当前位置：行情资讯 > 行业资讯 基于数值模拟的LED键合线热应力分析

摘要：

LED(Light-Emitting-Diode )以其高光效、低功耗的绿色节能优越性，成为新时期下的主流光源。目前LED主要依赖于引线键合(Wire-Bonding)的方式将芯片电极与基板互连实现电气连接，而键合线往往在冷热冲击试验过程中出现断裂问题，导致LED死灯失效，严重影响了LED的可靠性。本文针对这一问题，通过有限元数值分析，通过加载周期性的温度载荷模拟LED键合线在冷热冲击下受到的热载荷，分析了LED键合线在该热载荷条件下的应力分布情况，并探讨了不同引线线弧模式对键合线热应力的影响，为LED引线键合的工艺优化提供了参考。

　　序言

　　LED是一种直接将电能转化为光能的半导体光源，具有节能、环保、安全、寿命长、低功耗等特点，广泛应用于指示、显示、装饰、背光源、普通照明等领域^[1]。其芯片与基板之间通常采用引线键合进行电气连接，即通过热、压力、超声波等能量使金属引线与被焊焊盘发生原子间扩散互溶，实现芯片电极-键合线-基板彼此之间的键合连接。

　　在LED的生产制造中，为了解、评价、分析和提高LED的环境适应性，常对LED进行相关可靠性试验^[2]，冷热冲击试验即为其中一种。该实验通过对LED施加周期性瞬变的冷热温度循环，试验其所能承受的因热胀冷缩所引起的化学变化或物理伤害。在该试验中，LED键合线常成为其中的薄弱部位，其在试验中的断线与否对LED可靠性起着关键性作用。

　　为了了解LED键合线在冷热冲击试验下的断裂机理，本文从材料的热应力基础理论出发，构建冷热冲击条件下的LED键合线模型，并通过有限元数值模拟对键合线的热应力进行计算分析，进而确认键合线热应力分布情况及影响热应力的相关参数。

　　1 热应力基础理论

　　热应力又称温变应力。产生热应力的必要条件是存在温差，当温差引起的结构形变受到约束时即可产生热应力。约束有三种形式，即外部刚性约束、内部各部分之间变形约束以及不同材料之间的相互变形约束。对于LED而言，冷热冲击条件下，LED受到周期性的热胀冷缩，各材料之间热膨胀系数不同又相互约束，因此在各材料界面，极易产生应力集中。

　　根据线性热应力理论，微元体的总应变由两部分组成：一部分由温度变化引起，另一部分由应力引起，即：

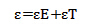
　　根据传热学原理，一维等截面杆由温度产生的结构形变(即热应变εT)为：

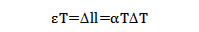
　　其中，αT-材料线膨胀系数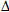，T-温差，l-一维方向初始长度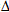，l-长度变化。

　　对于各向同性的三维结构，以上应变在各个方向均相同，但并不产生剪应变，即存在：

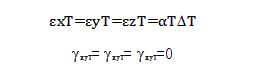
　　因此，平面结构(即εzT=0时)的热应变为：

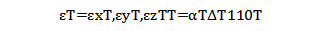
　　而弹性应变是由应力引起的：

　　所以在存在热应变的情况下，结构物理方程为：

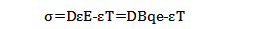
　　式中，D-计算平面应力问题的弹性矩阵，B-应变矩阵。根据弹性力学公式：

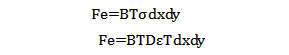
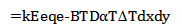
　　写成矩阵形式写成：

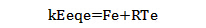
　　这里的kEe和Fe是平面应力问题中的单元刚度矩阵和节点力矩阵。

　　式中RTe是由于温度变化而增加的单元变温等效节点载荷矩阵。

　　通过求解温度方程求出各个节点的温度值以后，就可以求出温度载荷，式中单元的温升可以取各个节点的温升的平均值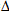T，即：

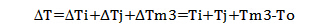
　　式中Ti、Tj、Tm—计算出的节点温度;

　　To—结构的初始温度

　　将求解域中所有单元的变温等效节点载荷叠加后，形成整个结构的温度载荷阵列，即：

　　RT=e=1nRTe

　　最后，将得到的温度变化RT视为一种温度载荷，并形成温度载荷列阵后，就可以按与静力分析相同的方法求解热变形，则求解热变形的刚度方程为：

　　Kq=RT

　　解上式可以求出结构的热变形q，进而能求出相应的热应力。

　　在冷热冲击过程中，由于LED封装体各部分组件材料的热膨胀系数不同，将产生周期性的膨胀与收缩。键合线会受到不同程度的剪切和拉伸，在键合线三维结构中应力呈多轴状态分布，因而在分析键合线在冷热冲击温度循环条件下的力学行为时，采用表示综合应力强度的等效应力来描述键合线的应力分布状态。

　　基于第四强度理论 Von Mises准则，等效应力用应力张量的分量表示为：

　　σ=22σx-σy2+σy-σz2+σx-σz2+6τxy2+τyz2+τxz212

　　式中σ—等效应力(Pa);

　　σx—X 方向正应力(Pa);

　　σy—Y 方向正应力(Pa);

　　σz—Z 方向正应力(Pa);

　　τxy—垂直于 X 轴平面的 Y 方向剪应力(Pa);

　　τyz—垂直于 Y 轴平面的 Z 方向剪应力(Pa);

　　τxz—垂直于 X 轴平面的 Z 方向剪应力(Pa)

　　由上述分析可知，对于LED而言，环境温度温差越大、封装材料之间的热膨胀系数相差越大、材料的弹性模量越大，LED受到热应力越大，随着时间增加，材料界面应力集中容易产生疲劳断裂。

　　当赋予LED各封装材料以热力学属性，施加材料的热边界条件，即可由以上各公式对LED三维模型的等效热应力进行分析求解，便可得出热载荷条件下LED各封装材料各位置的等效应力情况。其中，分析求解过程可通过有限元数值模拟求解实现^[3-5]。

 ...